having-fun-tickling-algorithms

Table of Contents

• Table of Contents
• 22. Generate Parentheses
  • Approach 1: Backtracking
  • Approach 2: DP
• 15. 3Sum
  • Approach 1: Two-pointers
  • Approach 2: Hashset + two-pointers
• 451. Sort Characters By Frequency
  • Approach 1: MaxHeap (priority queue)
  • Approach 2: array indexing
• 347. Top K Frequent Elements
  • Approach 1: MaxHeap (priority queue)
  • Approach 2: MinHeap
• 1155. Number of Dice Rolls With Target Sum
  • Approach 1: Dynamic Programming
  • Approach 2: HashMap, recursion
• 78. Subsets
  • Approach 1: Backtracking
• 31. Next Permutation
  • Approach 1: smart Math algo
• 2. Add Two Numbers
  • Approach 1: Math
• 445. Add Two Numbers II
  • Approach 1: Stack
• 200. Number of Islands
  • Approach 1: recursively changing the land to water
  • Approach 1:
  • Approach 1:
  • Approach 1:
  • Approach 1:
  • Approach 1:
  • Approach 1:

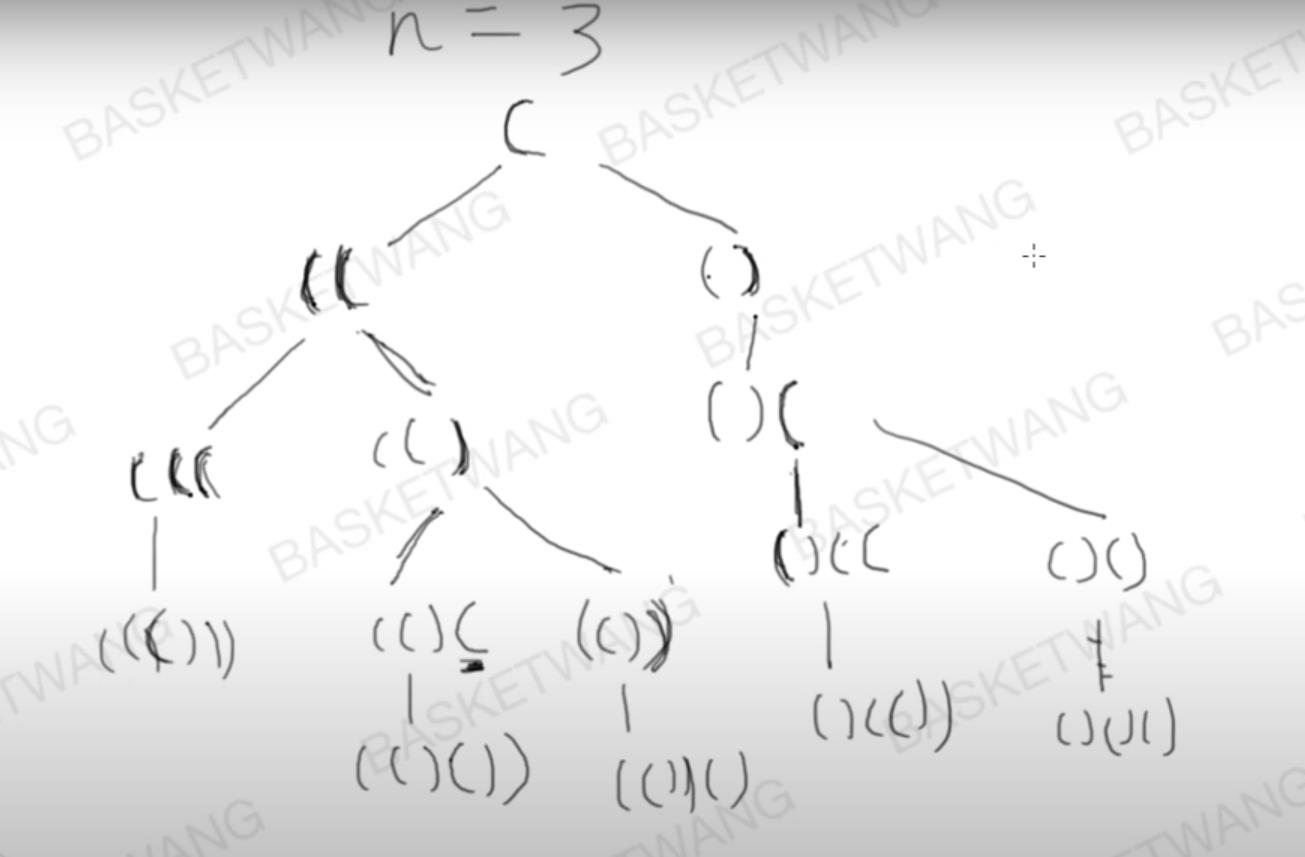
22. Generate Parentheses

Approach 1: Backtracking

Complexity Analysis:

class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> ans = new ArrayList<>();
        backtrack(ans, n, 0, 0, "");
        return ans;
    }

    public void backtrack(List<String> ans, int max, int open, int closed, String s) {
        if (max * 2 == s.length()) {
            ans.add(s);

        }
        if (open < max) {
            backtrack(ans, max, open + 1, closed, s + "(");
        }
        if (closed < open) {
            backtrack(ans, max, open, closed + 1, s + ")");
        }
    }
}

Approach 2: DP

First consider how to get the result f(n) from previous result f(0)…f(n-1). Actually, the result f(n) will be put an extra () pair to f(n-1). Let the “(“ always at the first position, to produce a valid result, we can only put “)” in a way that there will be i pairs () inside the extra () and n - 1 - i pairs () outside the extra pair.

Let us consider an example to get clear view:

f(0): ""

f(1): "("f(0)")"

f(2): "("f(0)")"f(1), "("f(1)")"

f(3): "("f(0)")"f(2), "("f(1)")"f(1), "("f(2)")"

So f(n) = "("f(0)")"f(n-1) , "("f(1)")"f(n-2) "("f(2)")"f(n-3) ... "("f(i)")"f(n-1-i) ... "(f(n-1)")"

public class Solution
{
    public List<String> generateParenthesis(int n)
    {
        List<List<String>> lists = new ArrayList<>();
        lists.add(Collections.singletonList(""));

        for (int i = 1; i <= n; ++i)
        {
            final List<String> list = new ArrayList<>();

            for (int j = 0; j < i; ++j)
            {
                for (final String first : lists.get(j))
                {
                    for (final String second : lists.get(i - 1 - j))
                    {
                        list.add("(" + first + ")" + second);
                    }
                }
            }

            lists.add(list);
        }

        return lists.get(lists.size() - 1);
    }
}

15. 3Sum

Approach 1: Two-pointers

for each arr[i], look at the rest of the array to see if there is a pair.

Idea: [-1,0,1,2,-1,-4] Loop through the sorted array, Look at -1, check if there are a pair of ints in the rest of the array that addes up to 1, then look at 2, check if there is a pair of ints ….

• Time complexity : O(n^2)
• Space complexity : O(n^2)

 public List<List<Integer>> threeSum(int[] nums) {
        Arrays.sort(nums);
        List<List<Integer>> output = new LinkedList();

        for(int i = 0; i < nums.length - 2; i++){
            if (i == 0 || i > 0 && nums[i] != nums[i-1]){
                int sum = 0 - nums[i];
                int left = i+1;
                int right = nums.length - 1;

                while (left < right){
                    if (nums[left] + nums[right] == sum){
                        output.add(Arrays.asList(nums[i], nums[left], nums[right]));
                        while(left < right && nums[left] == nums[left+1]){
                            left ++;
                        }
                        while(left < right && nums[right] == nums[right-1]){
                            right --;
                        }
                        left ++;
                        right --;
                    }else if(nums[left] + nums[right] > sum){
                        right --;
                    }else{
                        left ++;
                    }
                }
            }
        }
        return output;
    }

Approach 2: Hashset + two-pointers

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        Set<List<Integer>> set = new HashSet<>();
        if(nums.length == 0){
            return new ArrayList<>(set);
        }
        Arrays.sort(nums);

        for(int i = 0; i < nums.length; i ++){
            int left = i+1, right = nums.length - 1;
            while (left < right){
                int sum = nums[i] + nums[right]+nums[left];
                if (sum == 0){
                    set.add(Arrays.asList(nums[i], nums[right], nums[left]));
                    left ++;
                    right --;
                }else if (sum < 0){
                    left ++;
                }else if (sum > 0){
                    right --;
                }
            }
        }
        return new ArrayList<>(set);
    }
}

451. Sort Characters By Frequency

Approach 1: MaxHeap (priority queue)

• Time: O(n) + K*log(k)
  • Traverse each character of the string. That is O(n). n is the length of string.
  • Populate the heap with k distinct characters of the string. This klog(k). k is the number of distinct characters of the string. For example, “tree” is k is 3.
  • Append each character of the string. (k distinct characters _ the frequency) . That is O(n). So the total time complexity is 2 _ O(n) + Klog(k) = O(n) + Klog(k)
• Space: O(n)

class Solution {
    public String frequencySort(String s) {
        HashMap<Character, Integer> map = new HashMap();
        char[] chars = s.toCharArray();
        for(char c: chars){
            map.put(c, map.getOrDefault(c, 0) + 1);
        }
        //max heap building
        PriorityQueue<Character> maxHeap = new PriorityQueue<>((a, b) -> map.get(b) - map.get(a));
        maxHeap.addAll(map.keySet());
        StringBuilder sb = new StringBuilder();
        //loop through the maxHeap
        while(maxHeap.isEmpty() == false){
            char curr = maxHeap.remove();
            for(int i = 0; i < map.get(curr); i ++){
                sb.append(curr);
            }
        }

        return sb.toString();
    }
}

Approach 2: array indexing

• Build a map of characters to the number of times it occurs in the string
• Create an array where the index of the array represents how many times that character occurred in the String
• Iterate from the end of the array to the beginning, and at each index, append each character to the return string that number of times.
• Time: O(n)

347. Top K Frequent Elements

Approach 1: MaxHeap (priority queue)

use maxHeap. Put entry into maxHeap so we can always poll a number with largest frequency It is n[log n] because on a worst case if none of element repeat in input, you can have all the elements in heap. so, i.e all the ‘n’ elements are in the heap.

• Time: O(NlogK), since we do not need to insert to min heap n times, just k times. And poll() is O(1).

• Space: O(n + k)

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        Arrays.sort(nums);
        HashMap<Integer, Integer> map = new HashMap();
        for(int i = 0; i < nums.length; i ++){
            map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
        }

        //max heap
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> map.get(b) - map.get(a));
        maxHeap.addAll(map.keySet());

        int[]output = new int[k];
        while(!maxHeap.isEmpty() && k - 1 >= 0){
            int curr = maxHeap.remove();
            output[k-1] = curr; //k-1 -> 0
            k--;
        }
        return output;
    }
}

Approach 2: MinHeap

so that the heap size can be maintained <= k.

  public List<Integer> topKFrequent(int[] nums, int k) {
        Map<Integer, Integer> map = new HashMap<>();
        for(int n: nums){
            map.put(n, map.getOrDefault(n,0)+1);
        }

        PriorityQueue<Map.Entry<Integer, Integer>> minHeap =
            new PriorityQueue<>((a, b) -> Integer.compare(a.getValue(), b.getValue()));
        for(Map.Entry<Integer,Integer> entry: map.entrySet()){
            minHeap.add(entry);
            if (minHeap.size() > k) minHeap.poll();
        }

        List<Integer> res = new ArrayList<>();
        while(res.size()<k){
            Map.Entry<Integer, Integer> entry = minHeap.poll();
            res.add(entry.getKey());
        }
        return res;
    }

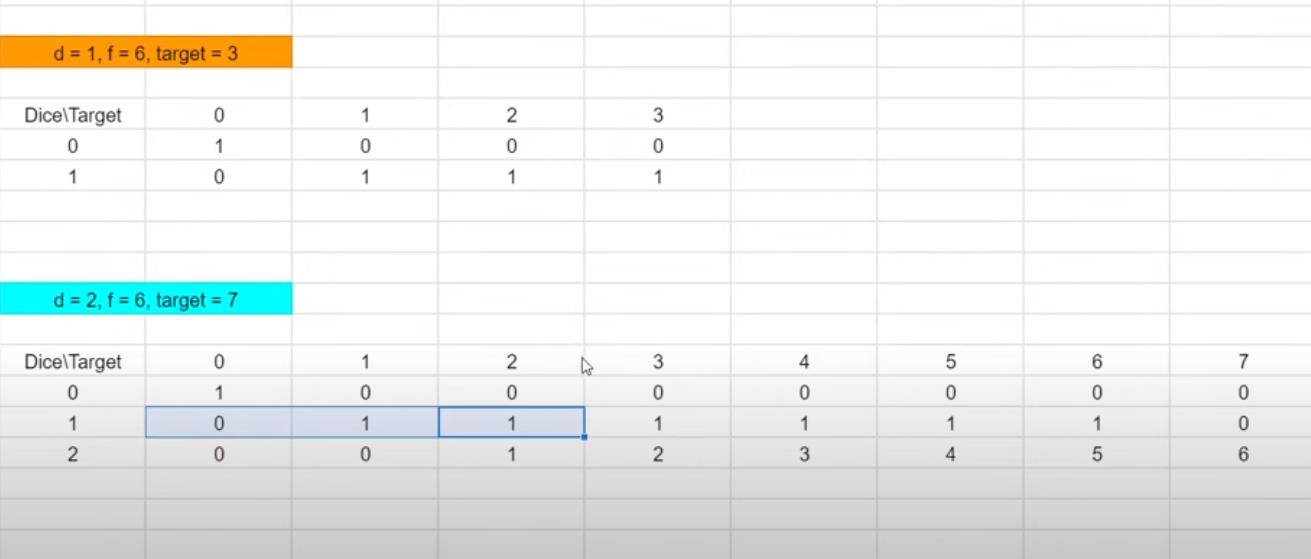
1155. Number of Dice Rolls With Target Sum

Approach 1: Dynamic Programming

• Time complexity: O(n*k*target)

• Space complexity:

Approach 2: HashMap, recursion

• Time complexity:

• Space complexity:

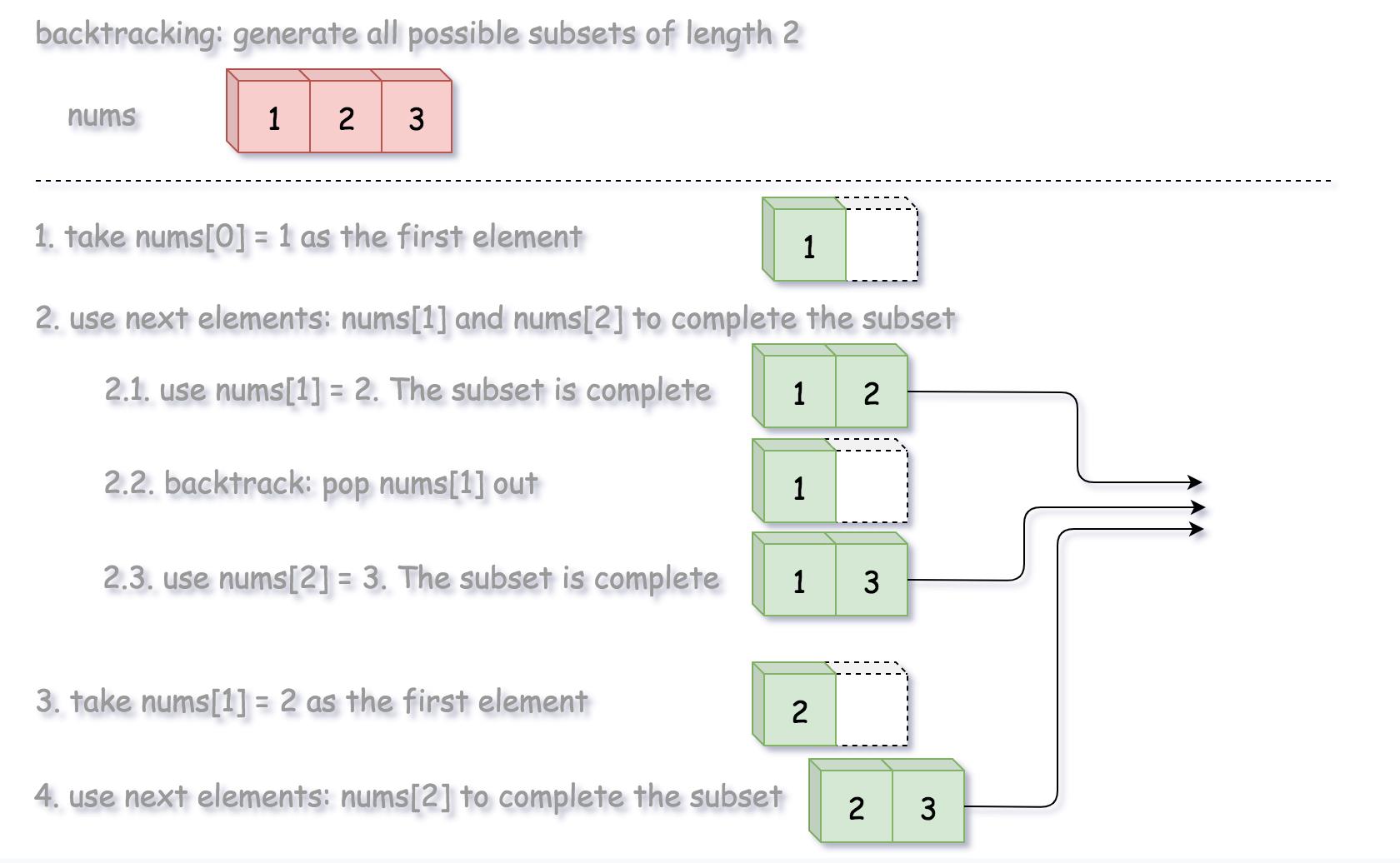
78. Subsets

Approach 1: Backtracking

>

• Time complexity:O(2^n), n is size of nums. the recursive call where you have index+1 should be i+1; Otherwise there would be duplicates.
• Space complexity: O(n), as the stack goes, the deepest of the stack could go would be the size of nums.

We define a backtrack function named backtrack(first, curr) which takes the index of first element to add and a current combination as arguments.

If the current combination is done, we add the combination to the final output.

Otherwise, we iterate over the indexes i from first to the length of the entire sequence n.

Add integer nums[i] into the current combination curr.

Proceed to add more integers into the combination : backtrack(i + 1, curr).

Backtrack by removing nums[i] from curr.

public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> powerset = new ArrayList<>();
        backtrack(nums, powerset, 0, new ArrayList<Integer>());
        return powerset;
    }
    //generate the powerset of the subset
public void backtrack(int[] nums, List<List<Integer>> powerset, int index, List<Integer> curr){
        powerset.add(new ArrayList<>(curr));
        for(int i = index; i < nums.length; i++ ){
            curr.add(nums[i]);
            backtrack(nums, powerset, i + 1, curr);
            curr.remove(curr.size() - 1);
        }
    }

31. Next Permutation

Approach 1: smart Math algo

1. find the first decreasing sequence starting from the end //a[i]a[i] and a[i-1]a[i−1] where, a[i] > a[i-1]a[i]>a[i−1]
2. find the the number which is just larger than itself among the numbers lying to its right section, say a[j], for substitution and perform swap
3. rearrange remaning array by reversing it

• Time complexity: O(n)
• Space complexity: O(1)

Note: 1) to find the first decreasing element, it has to be first >= 0 && nums[first] >= nums[first+1], so that we keep on looping when nums[first] is greater than or equal to nums[first+1]

1. Note that to find the next largest one in the rest of the decreasing array, we keep on looping whenever nums[justLargest] <= nums[first]

class Solution {
    public void nextPermutation(int[] nums) {
        int first = nums.length - 2;
        while (first >= 0 && nums[first] >= nums[first+1]){
            first --;
        }
        if (first >= 0){
            int justLargest = nums.length - 1;
            while (justLargest >= 0 && nums[justLargest] <= nums[first]){
                justLargest --;
            }
            swap (nums, justLargest, first);
        }
        //rearrange the remaning array by reversing it
        reverse(nums, first + 1);
    }
    public void swap(int[] nums, int i, int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
    public void reverse(int[] nums, int start){
        int end = nums.length - 1;
        while (start < end){
            swap(nums, start, end);
            start ++;
            end --;
        }
    }
}

2. Add Two Numbers

Approach 1: Math

• make a dummy node
• make a curr node pointing to the dummy node
• define carry to be 0
• while l1 is not null or l2 is not null,
  • if l1 is null, sum += l2.val + carry, and move l2 to next
  • if l2 is null, sum += l1.val + carry, and move l1 to next
  • else,
    • we compute sum = l2.val + l1.val + carry, and move both pointers to next
  • compute a node with sum%10 as its value
  • make curr.next pointing to the node
  • compute the carry to be sum/10
  • move curr one pointer foward.
• if ultimately the carry is remained,
• we create a carried node, and make curr.next pointing to it
• return result.next.

edge cases Null lists, lists of unequal length, handle sums involving carries , extra carry value at end

• Time complexity: O(max (N,M))
• Space complexity: O(max (N,M))

public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode result = new ListNode(-1);
        ListNode curr = result;
        int carry = 0;


        while (l1 != null || l2 != null){
            int sum = 0;
            if (l1 == null){
                sum += l2.val + carry;
                l2 = l2.next;
            }else if (l2 == null){
                sum += l1.val + carry;
                l1 = l1.next;
            }else{
                sum += l2.val + l1.val + carry;
                l1 = l1.next;
                l2 = l2.next;
            }
            int num = sum%10;
            carry = sum/10;
            curr.next = new ListNode(num);
            curr = curr.next;

        }
        if (carry > 0){
            ListNode carried = new ListNode(carry);
            curr.next = carried;
        }
        return result.next;
    }

445. Add Two Numbers II

Approach 1: Stack

• Time complexity:

• Space complexity:

 public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        Stack<Integer> stack1 = new Stack<>();
        Stack<Integer> stack2 = new Stack<>();

        while (l1 != null){
            stack1.push(l1.val);
            l1 = l1.next;
        }
        while (l2 != null){
            stack2.push(l2.val);
            l2 = l2.next;
        }
        int sum = 0;
        ListNode list = new ListNode(0);
        while (!stack1.isEmpty() || !stack2.isEmpty()){
           if (!stack1.isEmpty()){
               sum += stack1.pop();
           }
           if (!stack2.isEmpty()){
               sum += stack2.pop();
           }
           list.val = sum%10;
           ListNode head = new ListNode(sum/10);
           head.next = list;
           list = head;
           sum /= 10;
        }
        return list.val == 0?  list.next : list;
    }

200. Number of Islands

Approach 1: recursively changing the land to water

• keep track of count
• every time encounter 1, increase count,
  • call a recursive function to changes all 1s that are connected to the 1 to 0s
• because we don’t wanna repeatedly add the same island
• if out of bounds or it’s 0, we won’t be recurring.
• recursively call on each direction.

The time complexity is O(cells). Every cell is inspected at least once, due to the nested for loops. Any single cell is inspected at most 5 times. We know this because there are 5 ways a cell (i, j) can be inspected:

inspected in the nested for loop, before dfs is called
dfs from cell (i + 1, j)
dfs from cell (i - 1, j)
dfs from cell (i, j + 1)
dfs from cell (i, j - 1)
The nested for loops obviously inspect each cell exactly once.

dfs(i, j) exits immediately if (i, j) has been inspected already, which implies (i, j) can only be visited from dfs(i + 1, j) once, visited from dfs(i - 1, j) once, visited from dfs(i, j + 1) once, and visited from (i, j - 1) once.

• Time complexity: O(N^2), where N is the number of all the grids To be more accurate, it’s MN, where M is the number of all the ‘1’s

• Space complexity: O(N*m), worst case whole grid is filled with ‘1

 public int numIslands(char[][] grid) {
        if (grid == null) return 0;
        int count = 0;
        for(int i = 0; i < grid.length; i ++){
            for(int j = 0; j < grid[0].length; j++){
                if (grid[i][j] == '1'){
                     count ++;
                     changeLandtoWater(grid, i , j);
                }
            }
        }
        return count;
    }
private void changeLandtoWater(char[][] grid, int i, int j){
        if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] == '0') return;
        grid[i][j] = '0';
        changeLandtoWater(grid, i - 1, j);
        changeLandtoWater(grid, i , j - 1);
        changeLandtoWater(grid, i + 1, j);
        changeLandtoWater(grid, i, j +1);

}

##

Approach 1:

• Time complexity:

• Space complexity:

##

Approach 1:

• Time complexity:

• Space complexity:

##

Approach 1:

• Time complexity:

• Space complexity:

##

Approach 1:

• Time complexity:

• Space complexity:

##

Approach 1:

• Time complexity:

• Space complexity:

##

Approach 1:

• Time complexity:

• Space complexity: